انحراف استاندارد

همان طور که در مقاله دقت و صحت گفته شد انحراف استاندارد (standard deviation) پرکاربردترین معیار برای اندازه گیری دقت اندازه گیری ست. این واژه یکی از پارامترهای اصلی در منحنی خطای نرمال یا گوسین (normal error or Gaussian curve) است.

منحنی خطای نرمال

برای فهم درست انحراف استاندارد یا انحراف معیار لازم است تا کمی در مورد منحنی خطای نرمال یا منحنی گوسین بیشتر بدانیم:

شکل 1 دو منحنی برای توزیع فراوانی دو مجموعه تئوری داده را نشان می دهد که هر یک دارای تعداد بی نهایت مقادیر است و به عنوان یک جامعه آماری (statistical population) شناخته می شوند.

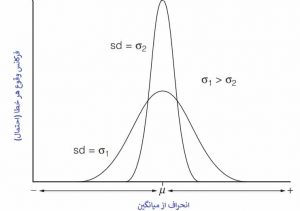
مقدار ماکزیمم (قله) در هر منحنی با میانگین جمعیت مطابقت دارد، که برای این نمونه ها مقدار یکسانی دارد (µ). با این حال، گستردگی یا پراکندگی مقادیر برای این دو مجموعه کاملاً متفاوت است و این موضوع در نیمه پهنای دو منحنی در نقاط عطف منعکس می شود که طبق تعریف، انحراف استاندارد جمعیت (σ) است. از آنجا که σ₂ بسیار کمتر از σ₁ است، دقت مجموعه دوم بسیار بهتر از مجموعه اول است. مقیاس منحنی X را می توان در واحد های مطلق یا معمولاً به صورت انحراف مثبت و منفی از میانگین درجه بندی کرد.

به طور کلی، هرچه گستردگی مقادیر یا انحرافات کوچک تر باشد ، مقدار σ کوچک تر است و از این رو دقت بهتری خواهد داشت. در عمل، هرگز نمی توان مقادیر واقعی µ و σ را شناخت زیرا با جمعیتی به اندازه بی نهایت ارتباط دارند. با این حال، فرضیه ای مطرح می شود که تعداد کمی از مقادیر آزمایشی یا یک نمونه آماری که از یک جامعه آماری گرفته شده است اغلب توزیع یکسانی خواهند داشت. بنابراین میانگین تجربی (x بار) ، از مجموعه مقادیر x₁ ، x₂ ، x₃ ،x_n…….. به عنوان برآورد میانگین واقعی یا جمعیت (µ) و انحراف معیار آزمایشی (s) تخمینی از انحراف معیار واقعی یا جمعیت (σ) در نظر گرفته می شود.

یک ویژگی مفید منحنی خطای نرمال این است که، صرف نظر از مقدار µ و σ ، سطح زیر منحنی در محدوده های مشخص شده در هر دو طرف µ (که معمولا به صورت مضربی از  σ ± بیان می شود)  یک ثابتی متناسب با کل مساحت منحنی ست که به برحسب درصد بیان می شود و درصد جمعیت دو محدوده را مشخص می کند. بنابراین، تقریبا 68٪ مساحت و جمعیت در محدود c±1σ از میانگین، تقریبا 95٪ مساحت و جمعیت در محدود c±2σ از میانگین، و تقریبا 99.7٪ مساحت و جمعیت در محدود c±3σ از میانگین، یافت می شوند. شکل 2 سطوح مربوط به 90٪ ، 95٪ و 99٪ از جمعیت را  که به ترتیب با  ±2.58σا ,c±1.96σ و c±1.64σ تعریف می شوند را نشان داده است. بسیاری از آزمون های آماری بر اساس این سطوح احتمال تعریف می شوند.

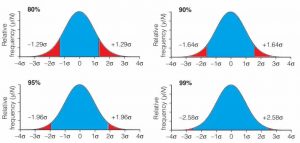
شکل 2 نسبت جمعیت در محدوده تعریف شده میانگین

فرمول انحراف استاندارد

مقدار انحراف استاندارد جمعیت از فرمول زیر محاسبه می شود:

$\sigma =\sqrt{\frac{\sum _{i=1}^{i=N}{(x_i–\mu )}^2}{N}}$

که در آن  x_i   یک مقدار مشخص را در جمعیت نشان می دهد و N تعداد کل جمعیت ( تا بی نهایت) است. علامت جمع ، سیگما Σ، برای نشان دادن این است كه معادله حاصل جمع i = 1 تا i = N از جمع مربعات انحرافات مقادیر ویژه x از میانگین جمعیت است، استفاده می شود. برای مجموعه داده های بسیار بزرگ ( مثلا وقتی که N>50) ، ممکن است استفاده از این فرمول قابل توجیه باشد زیرا تفاوت بین s و σ ناچیز خواهد بود. اما در عمل تعداد اندازه گیری ها اغلب کمتر از ده و معمولا با سه بار تکرار است. بنابراین، از فرمول اصلاح شده برای محاسبه انحراف معیار استاندارد ، s ، برای جایگزینی σ و استفاده از میانگین تجربی ، (x بار)، برای جایگزینی میانگین جمعیت، µ استفاده می شود.

مقدار انحراف استاندارد نمونه از فرمول زیر محاسبه می شود:

$s=\sqrt{\frac{\sum _{i=1}^{i=N}{(x_i–\overline{x})}^2}{N–1}}$

توجه داشته باشید که N در مخرج با N – 1 جایگزین می شود، که به عنوان تعداد درجه آزادی (degree of freedom) شناخته می شود. درجه آزادی تعداد انحراف های مستقل (xi-x) محاسبه s تعریف می شود. برای مجموعه های داده تکی، درجه آزادی همیشه یک عدد کمتر از تعداد مجموعه داده یا N-1 است .

به طور خلاصه ، محاسبه انحراف استاندارد ، برای تعداد کمی از مقادیر شامل مراحل زیر است:

• محاسبه میانگین تجربی (x بار)
• محاسبه انحراف تک تک مقادیر x_i از میانگین
  $(x_i–\overline{x})$
• مربع انحرافات و جمع بندی آنها
  $\sum _i^N{(x_i–\overline{x})}^2$
• تقسیم بر تعداد درجه آزادی ، N – 1 و جذر مربع نتایج بالا (فرمول 2)

محاسبه انحراف استاندارد در اکسل

محاسبه انحراف معیار به راحتی با ماشین حساب های مهندسی انجام می شود. به علت کاربرد زیاد این پارامتر بسیاری از نرم افزارهای عمومی نیز تابع محاسبه مقادیر انحراف معیار را دارند.

توابع زیر انحراف معیار نمونه را محاسبه می کنند:

• STDEV
• STDEV.S
•  STDEVA (مقادیر متنی و منطقی را نیز ارزیابی می کند)

توابع زیر انحراف معیار جمعیت را محاسبه می کنند:

• STDEVP
• STDEV.P
• STDEVPA (مقادیر متنی و منطقی را نیز ارزیابی می کند)

انحراف استاندارد نسبی

انحراف استاندارد نسبی (relative standard deviation) ، RSD یا s_r، به عنوان ضریب تغییر (coefficient of variation) CV نیز شناخته می شود. انحراف استاندارد نسبی  یک معیاری از دقت نسبی است و به طور معمول به صورت درصدی از مقدار متوسط یا نتیجه بیان می شود:

$s_r=\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$\overline{x}$}\right.\right)\times 100$

پس انحراف استاندارد نسبی (ضریب تغییر) انحراف استانداردی است که به عنوان درصدی از مقدار اندازه گیری شده بیان می شود.

انحراف استاندارد ادغام شده

در مواردی که نمونه های تکراری در موارد مختلفی تحت همان شرایط مشخص آنالیز می شوند ، می توان با تجمیع داده ها از مجموعه های مختلف، برآورد بهبود یافته از انحراف استاندارد را به دست آورد. یک فرمول کلی برای انحراف استاندارد تجمیعی یا انحراف استاندارد ادغام شده (pooled standard deviation)، با استفاده از معادله زیر ارائه می شود:

$s_{pooled}=\sqrt{\frac{{\displaystyle \underset{i=1}{\overset{i=N_1}{\sum (x_i–}}}\overline{x_1}{)}^2+\underset{i=1}{\overset{i=N_2}{\sum (x_i–}}{\overline{x}}_2{)}^2+ \underset{i=1}{\overset{i=N_3}{\sum (x_i–}}{\overline{x}}_3{)}^2+.....}{{\displaystyle \sum _{i=1}^{i=k}}{N}_i}}$

 

که در آن N₁, N₂, N₃, N₄, …. تعداد نتایج در k مجموعه و x بارها میانگین هر مجموعه است. انحراف استاندارد را می توان برای دو یا چند مجموعه داده با تجمیع مقادیر محاسبه کرد تا اندازه گیری دقیق تری داشته باشد.

واریانس

مربع انحراف استاندارد یا s² را واریانس (Variance) گویند. واریانس در برخی از آزمون های آماری استفاده می شود.

var=s²

دقت کلی

خطاهای تصادفی جمع شده در یک روش آنالیزی در دقت کلی (Overall precision) سهیم هستند. در مواردی که نتیجه محاسبه شده با جمع یا تفریق مقادیر منفرد بدست می آید، می توان با جمع بندی واریانس همه اندازه گیری ها، نتیجه کلی را بدست آورد تا برآوردی از انحراف استاندارد کلی را ارائه دهد، یعنی

$s_{overall=\sqrt{(s_1^2+s_2^2+s_3^2+s_4^2+....}}$

که S₁²و … واریانس خطاهای منفرد هستند.