یکی از متداول ترین روش های آنالیز فاکتوری (Factor analysis) یا بررسی عاملی، روش تجزیه مولفه های اصلی (principal component analysis) با نام اختصاری و متداول PCA است. این روش در بسیاری از زمینه های علوم شامل بیولوژی، کشاورزی، اقتصاد، گرافیک، شیمی، علوم اجتماعی و رفتاری و غیره جهت تشخیص الگو (pattern recognition)، دسته بندی (Clustering) و طبقه بندی (classification)، مدل سازی نرم (soft modeling) و ..کاربرد گسترده ای دارد.
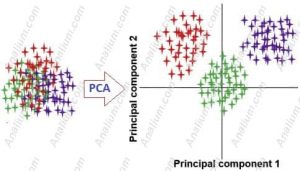
اصول تجزیه مولفه های اصلی (PCA)
شکل 1 مراحل اصلی روش PCA را به صورت گرافیکی نشان می دهد. اولین قدم، یافتن بزرگترین جهت واریانس در ماتریس داده هاست که به آن مولفه اصلی اول یا به اختصار PC1 (First principal component) گویند. مولفه اصلی دوم یا PC2 به نحوی تعریف می شود که حداکثر واریانس موجود در داده ها را که توسط PC1 محاسبه نشده اند، را نشان دهد اما بر PC1 عمود باشد (شکل 1). مولفه های اصلی دیگر نیز به همین نحو انتخاب می شوند که حداکثر واریانس موجود در داده ها را نشان دهند اما بر مولفه های اصلی دیگر عمود باشند. عمود بودن PC ها یا مولفه های اصلی برهم یعنی اینکه مولفه های اصلی هیچ هم بستگی با هم ندارند و هم بستگی بین آنها صفر است.
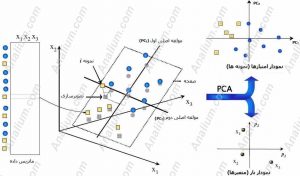
شکل 1 شمای گرافیکی روش تجزیه مولفه های اصلی (PCA)
داده اولیه معمولا، برای انتقال به مرکز سیستم مختصات و هم مقیاس شدن (scaling) متغیرها با هم، به پیش پردازش (preprocessing) نیاز دارند. رسم بهترین خط برازش شده (Best-fit line) از میان داده های اولیه، جهت حداکثر واریانس تصویر سازی شده روی خط (maximum variance of the projections onto the line) را نشان می دهد. این خط همان مولفه اصلی اول یا PC1 است. بنابراین PC1 ترکیب خطی (linear combination) از تمام متغیرهای اولیه است و می توان آن را به صورت زیر نوشت:
PC1=a11X1+a21X2+…..+ap1Xp
و همین طور برای PC2:
PC2= a12X1+a22X2+…..+ap2Xp
اندییس های a ضرایب متغیرها در مولفه های اصلی هستند.
توجه شود که مولفه اصلی اول (PC1) بیشترین واریانس داده ها را نشان می دهد و مولفه های اصلی بعدی، به ترتیب واریانس های کمتری، که در مولفه های اصلی قبلی لحاظ نشده، را نشان می دهند.
محاسبات روش PCA
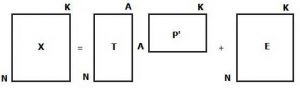
اساس محاسبات روش PCA تجزیه ماتریس اولیه (X) به دو ماتریس کوچک تر، ماتریس امتیاز و ماتریس بار، طبق معادله زیر است:
X=TP’+E
در رابطه بالا، T ماتریس امتیازها (scores)، P ماتریس بارها (loading) و E ماتریس باقی مانده یا خطا ست. شکل 2 تجزیه ماتریس X، با Nنمونه و K متغیر، به دو ماتریس امتیاز، با Nسطر و A ستون که A همان تعداد PC هست، و ماتریس بار، با A سطر و K ستون را نشان می دهد. در واقع ماتریس اولیه X به دو زیرفضای (subspace) کوچک تر با ابعاد d تصویرسازی می شود.
شکل 2 تجزیه ماتریس اولیه به دو ماتریس کوچک تر در روش PCA
فاصله اولیه هر نقطه تا نقطه تصویر شده آن بر روی این خط را امتیاز یا Score می گویند. بنابراین به هر مشاهده یا نمونه ای یک امتیاز تعلق می گیرد که ممکن است منفی یا مثبت باشد. ماتریس امتیاز در رابطه با علامت T نشان داده شده است.
در شکل 2 ماتریس بار را با علامت P نشان داده شده است.P’ نشانه ترنهاده ماتریس P است. ماتریس بار تصویرسازی متغیرها بر روی مولفه های اصلی ست.
برای تصویرسازی (projection) داده ها در PCA از الگوریتم های مختلفی مانند تجزیه بردارهای ویژه (eigenvector analysis)، تجزیه مقادیر منفرد (singular value decomposition) یا SVD و حداقل مربعات جزیی غیر خطی تکرار شونده (nonlinear iterative partial least squares) یا NIPALS استفاده می شود.
معمولا در بیشتر آنالیزهای PCA، چند مولفه اصلی اول درصد بالایی از تغییرات داده ها را نشان می دهند و نیازی به استفاده از تمام مولفه های اصلی نیست. با رسم مقادیر ویژه هر PC به تعداد PC ها، نمودار اسکری (Scree) به دست می آید که از محل شکستگی (inflection point) نمودار، می توان تعداد مولفه های اصلی لازم را به دست آورد (شکل 3). البته می توان مقادیر ویژه یا درصد واریانس را نیز به عنوان معیار در نظر گرفت. مولفه های اصلی با مقادیر ویژه بزرگتر از یک یا تعداد مولفه های اصلی با مجموع واریانس بیشتر از 90% را نگه داشته و بقیه را حذف کرد.

شکل3 نمودار اسکری (Scree) برای تعیین تعداد مناسب مولفه های اصلی در روش PCA
نمودار امتیاز (score plot) و نمودار بارها (loading plot) نتایج گرافیکی روش PCA هستند که به ترتیب از ماتریس امتیازها و ماتریس بارها به دست می آیند. با فرض اینکه نرم افزارهای رایگان و تجاری زیادی در دسترس هستند که قابلیت انجام آنالیز PCA را با چند کلیک دارند، مهم ترین قسمت تحلیل نمودارهای امتیاز و بار برای تفسیر و نتیجه گیری نهایی در مورد نمونه ها یا مشاهدات و متغیرها ست. نمودار امتیاز برای دسته بندی و تشخیص الگو بین مشاهدات و یا نمونه ها به کار می رود. از نمودار بار می توان همبستگی بین متغیرها را نیز بررسی کرد.
کاربرد PCA در آنالیز شیمیایی
بسیاری از دستگاه های مدرن امروزی حجم عطیمی داده در هر آنالیز تولید می کنند که آنالیز، تحلیل و تفسیر آنها بدون کمک روش های آماری تقریبا غیر ممکن است. به عنوان مثال طیف FT-IR شامل هزاران داده برای هر نمونه است. یا یک دستگاه GC-MS در هر آنالیز بیش از 600,000 اعداد دیجیتالی تولید می کند. استخراج اطلاعات مفید از این حجم بسیار بزرگ داده یک چالش جدی است. متاسفانه در بسیاری از مواقع به دلیل عدم آگاهی یا عدم تسلط به روش های کاهش داده ها فقط به درصد کمی از این داده ها توجه می شود. به عنوان مثال در روش اسپکتروسکوپی فقط ماکزیمم شدت طیف در نظر گرفته می شود.
روش PCA پایه اصلی بسیاری از تکنیک های کمومتریکس است. PCA ابزاری عالی برای تجزیه و تحلیل داده های چند متغیره در شیمی است. این مهم ترین روش برای تجزیه و تحلیل اکتشافی داده های چند متغیره کاهش ابعاد و نمایش گرافیکی داده ها است.
نکات تجزیه مولفه های اصلی (PCA)
- روشی توانمند در کاهش ابعاد داده ها، بدون از دست دادن اطلاعات زیاد، است.
- روش ساده ایست و کاربرد وسیعی در زمینه های مختلف علوم دارد.
- مولفه های اصلی (PC) همیشه عمود بر هم هستند بنابراین مشکل هم بستگی متغیرها در این روش اهمیتی ندارد.
- روش PCA می تواند تا 25% داده های گمشده (missing data) را تحمل کند.
- فرض اولیه در PCA بر رابطه خطی است در صورتی که امکان وجود داده غیر خطی نیز وجود دارد.