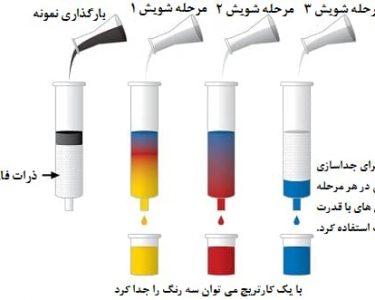
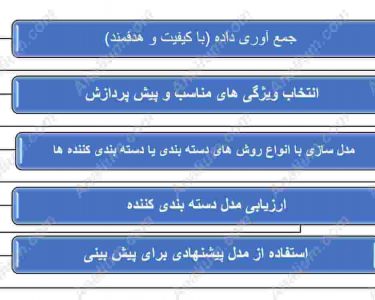
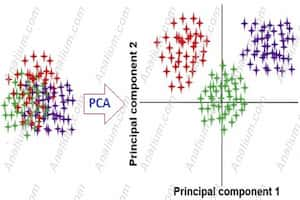
آزمون فرضیه (hypothesis testing)، یک روال رایج و کاربردی در علم داده هاست و کاربرد زیادی در بیشتر علوم مانند اقتصاد، علوم اجتماعی، زیست شناسی، شیمی، داروسازی و .. دارد. هدف آزمون فرضیه آماری این است که از یک فرضیه ابتدایی و خام، به یک گزاره و قضیه موثر برسیم و یا به عبارتی هدف اطمینان از این موضوع است که با توجه به اطلاعات به دست آمده از داده های نمونه، حدسی که درباره مشخصه ای از جامعه می زنیم قابل تایید است یا خیر؟ دقت کنید که فرض آماری، ادعایی در مورد یک یا چند جامعه مورد بررسی است که ممکن است درست یا نادرست باشد. تکنیک های آماری مناسب برای بررسی صحت فرضیه ها را آزمون فرضیه گویند.
نمونه و جامعه در آزمون فرضیه های آماری
قبل از هر بحثی بهتر است تعریف دقیق و شفافی در مورد دو اصطلاح رایج در آمار یعنی جامعه و نمونه داشته باشیم. اصطلاح جامعه یا جمعیت (population) زمانی استفاده می شود که یک نمونه برداری بی نهایت رخ داده یا همه افراد احتمالی مورد تجزیه و تحلیل قرار گرفته اند. بدیهی است که ما نمی توانیم اندازه گیری را بی نهایت بار تکرار کنیم ، بنابراین اغلب جامعه یک ایده نظری است و در این موارد ما یک نمونه نماینده (representative sample) از کل جامعه را می گیریم. به عنوان مثال، اگر بخواهیم از متوسط قد نژاد بشر مطلع شویم، باید نمونه ای نماینده از افراد گرفته شده و قد آنها را اندازه گرفت. نتیجه حاصل تخمینی از قد افراد جامعه است البته به همراه عدم قطعیت یا انحراف استاندارد نتیجه نهایی. اگر پارامترهای یک آزمایش به طور خاص تعریف شده باشد، می توان کل جامعه را تجزیه و تحلیل کرد. به عنوان مثال، اگر سوال این بود که میانگین قد خانواده نزدیک شما چقدر است؟ بنابراین جامعه شما به عنوان خانواده نزدیک شما تعریف شده است و می توان قد کل جامعه را اندازه گرفت. اما توجه کنید که خطای تصادفی مرتبط با هر اندازه گیری در جمع آوری داده ها در مورد کل جامعه نیز وجود دارد.
نکته دیگر این که کاربرد آماری کلمه نمونه (sample) از روش استفاده شیمیایی کلمه “نمونه” را باید تشخیص دهیم. به عنوان مثال، اگر بخواهیم خاک یک مزرعه را برای غلظت آرسنیک اندازه گیری کنیم، باید به مزرعه برویم و 20 “نمونه نماینده ” خاک را جمع آوری کرده و به آزمایشگاه بیاوریم. در واقع ما 20″نمونه” خاک از 20 نقطه از مزرعه جمع آوری کرده ایم. از نگاه آماری، 20 نمونه جمع آوری شده 20 داده برای نمونه برداری از کل جامعه، است و کل مجموعه 20 نقطه داده را نمونه می خواند. اگرچه گیج کننده است ولی اگر دقت کنید ساده است!!
فرض صفر و فرض مقابل
فرض آماری، یک ادعا یا گزاره ای در مورد توزیع یک جمعیت یا پارامتر توزیع یک متغیر تصادفی است. فرضیه آماری، نقطه آغاز آزمون فرض است و اصولا بدون داشتن فرضیه آماری امکان انجام یک آزمون دشوار است. فرض آماری ادعایی درباره جامعه است که قابل قبول بودن یا نبودن آن باید بر مبنای اطلاعات حاصل از نمونه گیری از جامعه بررسی شود. به این فرض یا ادعاها فرض صفر (null hypothesis) گفته می شود و آن را با H0 نشان می دهند. فرضیه صفر، حدس اولیه و اصلی ماست و فرض بر این است که در حال حاضر این فرضیه، معتبر است.
شکل –1 رابطه حدس و گمان علمی و فرض صفر
فرض آماری که در مقابل فرض صفر قرار می گیرد و نقض کننده فرض صفر است را فرض مقابل (alternative hypothesis) می نامند و آن را با H1 یا Ha نشان می دهند. فرض مقابل را با نام فرض اول یا فرض یک نیز نام گذاری می کنند. فرضیه جایگزین، فرضیه مخالف با فرضیه صفر است. اگر این فرضیه از لحاظ آماری تایید شود، به معنای رد شدن فرضیه صفر یا رد شدن فرضیه اولیه ما خواهد بود.
مثال
ادعا می شود که با اندازه گیری 50 نمونه آب های سطحی یک منطقه متوسط میزان سرب موجود در آب برابر با 32 ppb است. پس فرض صفر و فرض مقابل آن را می توان به صورت زیر نوشت:
H0: µ=32 , H1: µ#32
از آنجایی که توزیع یک جمعیت یا پارامتر توزیع یک متغیر تصادفی است پس منحنی توزیع نرمال یا منحنی گوسی پایه محاسبات ما خواهد بود.
توجه کنید که فرضیه های که در آنها اغلب جمعیت های مورد مقایسه دارای توزیع نرمال و واریانس های برابر هستند را آزمون های پارامتری گویند. اگرچه تعداد این نوع آزمون های آماری محدود است اما از آنجا که این شرایط در انواع جمعیت های مورد مطالعه وجود دارند در بیشتر مواقع از آنها استفاده می شود. در مقابل آزمون های ناپارامتری یا آزمون های توزیع آزاد برای سازگاری با شرایطی طراحی شده اند که در آنها جمعیت ها دارای توزیع نرمال نیستند و یا توزیع آنها شناخته شده نیست. اگر متغیرها عددی نبوده و از نوع اسمی و ترتیبی باشد حتما از روش های ناپارامتری استفاده می شود. در اینجا ما صرفا با آزمون های پارامتری که از توزیع نرمال تبعیت می کنند استفاده می کنیم.
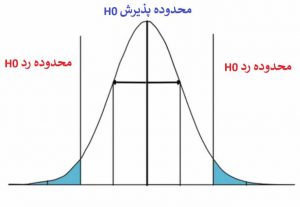
طبق شکل زیر توزیع آماره آزمون، به دو محدوده تقسیم می شود: محدوده پذیرش H0 و محدوده رد H0. ناحیه رد H0 را ناحیه بحرانی و مرز بین دو محدوده رد و قبول را مقادیر بحرانی می نامیم. در واقع مقادیر بحرانی، محدوده رد را از قبول جدا می کند.
برای اطلاعات بیشتر و مثال های کاربردی مقاله زیر را بخوانید: