انحراف استاندارد و خطای استاندارد

انحراف استاندارد و خطای استاندارد هر دو از پارامترهای مهم آماری هستند که  در زمینه های مالی، پزشکی، زیست شناسی، مهندسی، روانشناسی و … برای ارائه مشخصات داده های نمونه و توضیح نتایج تجزیه و تحلیل آماری مورد استفاده قرار می گیرند.  از نظر آماری انحراف استاندارد و خطای استاندارد دو مفهوم متفاوت هستند که متاسفانه در بسیاری از مواقع تفسیر نادرستی از مفاهیم این دو واژه صورت می گیرد. در بسیاری از مواقع انحراف استاندارد و خطای استاندارد به جای هم استفاده می شوند که همین امر منجر به تفسیرهای غلط از آزمون های آماری و نتیجه گیری نادرست از آزمایشات عملی می شود. برای این که بتوانیم در مورد تمایز و تفاوت محاسباتی و در نتیجه مفهومی انحراف استاندارد و خطای استاندارد صحبت کنیم یک بار دیگر به تعریف و فرمول هر کدام نگاهی می اندازیم:

انحراف استاندارد

برای جزییات بیشتر درباره انحراف  استاندارد این مقاله را بخوانید. برای یاد آوری انحراف استاندارد (Standard Deviation)  یا در برخی منابع انحراف معیار از رابطه زیر به دست می آید:

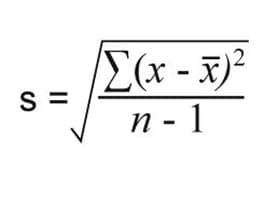
که در آن  x_i   یک مقدار مشخص را در جمعیت نشان می دهد و n تعداد کل جمعیت ( تا بی نهایت) است. علامت جمع ، سیگما Σ، برای نشان دادن این است كه معادله حاصل جمع i = 1 تا i = n از جمع مربعات انحرافات مقادیر ویژه x از میانگین جمعیت است، استفاده می شود.

خطای استاندارد

خطای استاندارد (Standard Error) و یا به بیان دقیق تر خطای استاندارد از میانگین (Standard error of the mean (SEM)) شاخصی برای تخمین میانگین جمعیت است. خطای استاندارد  و یا در برخی منابع خطای معیار از رابطه زیر به دست می آید.پ

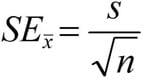
که در آن s انحراف استاندارد و n تعداد نمونه است. SEM تغییرات برآورد ما از میانگین را نشان می دهد و هرچه تعداد نمونه افزایش یاید این تغییرات کاهش می یابد. خطای استاندارد با اندازه گیری تنوع نمونه به نمونه از میانگین نمونه ، دقت میانگین نمونه را نشان می دهد. SEM میزان دقیق نمونه را به عنوان برآورد میانگین واقعی جمعیت توصیف می کند. از این رو ، با افزایش اندازه نمونه ، میانگین نمونه میانگین دقیق جمعیت را با دقت بیشتری تخمین می زند.

تفاوت انحراف استاندارد و خطای استاندارد

برای اینکه تفاوت انحراف استاندارد و خطای استاندارد بهتر متوجه شویم با یک مثال ادامه می دهیم: فرض کنید میخواهیم میزان متوسط قد  زنان ایران را بررسی کنیم و از نظر عملیاتی امکانات توانایی انجام اندازه گیری قد کل جمعیت زنان ایران  را داریم. اگر توزیع اندازه گیری قد این جمعیت (40 میلیون و حدود نصف جمعیت ایران) را رسم کنیم شکلی  گوسی یا نرمال به دست می آید که با دو تا پارامتر میانگین و انحراف معیار مشخص می شود. اما در عمل امکان اندازه گیری قد تمام زنان ایرانی امکان پذیر نیست. پس مجبور خواهیم بود که بخش کوچکی از زنان جامعه ایران انتخاب کنیم و قد انها را برای تجزیه و تحلیل اندازه گیری کنیم. به این صورت که یک جامعه آماری از هر شهر انتخاب می شود. در این حالت به جای یک مجموعه تعدادی زیر مجموعه خواهیم داشت. در واقع متوسط قد زنان در شهرهای مختلف متفاوت خواهد بود. در نتیجه هر جامعه ای میانگین و انحراف معیار متفاوتی خواهد داشت. شکل زیر نمای شماتیک تفاوت این دو واژه را نشان می دهد:

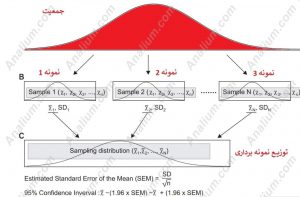
پس به صورت خلاصه تفاوت انحراف استاندارد و خطای استاندارد عبارتند از:

• انحراف استاندارد یکی از شاخصه های اصلی برای توصیف داده‌ها  و یا آمارتوصیفی ست اما خطای استاندارد یا SE از  شاخصه های  آمار استنباطی ست و برای انجام استنباط راجع به داده‌ها به کار می رود.
• خطای استاندارد و انحراف استاندارد هر دو معیارهای برای توصیف تغییر هستند. انحراف استاندارد نشان دهنده تغییر موجود در یک نمونه است ، در حالی که خطای استاندارد تغییرموجود در نمونه های یک جمعیت مشخص می کند.
• SD با افزایش تعداد نمونه ثابت اما SE با افزایش تعداد نمونه کاهش می‌یابد. در مقابل ، افزایش تعداد نمونه لزوماً SD را بزرگ یا کوچک نمی کند ، بلکه به برآورد دقیق تری از SD جمعیت تبدیل می شود.
• SD فقط برای جامعه‌های دارای توزیع نرمال ارائه و برای جامعه‌های غیرنرمال از دامنه میان چارکی (فاصله بین چارک اول و سوم) استفاده می‌شود.
• SD به تنهایی دارای مفهوم مستقل است اما SE به تنهایی فاقد مفهوم بوده و در قالب فاصله اطمینان ارائه می‌شود.
• مقدار SE همواره کوچک‌تر از SD است و متاسفانه همین مقدار کمتر استفاده از آن به جای SD باعث فریب خواننده و مناسب جلوه دادن داده‌ها می‌شود.
• اگر بخواهیم در مورد گسترش و تغییرپذیری داده ها نتیجه گیری کنیم ، باید از انحراف استاندارد یا انحراف معیار استفاده کنیم اما اگر می خواهید دقیق بودن میانگین نمونه را پیدا کنید یا تفاوت های بین دو روش را آزمایش می کنید ، معیار شما خطای استاندارد است.

نحوه کاربرد صحیح انحراف استاندارد و خطای استاندارد

انحراف معیار، پراکندگی (تغییر پذیری) داده ها را با توجه به میانگین اندازه گیری می کند. به عبارت ساده تر، هرچه  انحراف استاندارد  کمتر باشد پراکندگی حول میانگین کمتر بوده و داده ها به مقدار میانگین نزدیک ترند. همانطور که در مقاله انحراف استاندارد گفته شد، توزیع استاندارد اطلاعات ارزشمندی را از نظر درصد داده های واقع در 1 ، 2 ، 3 (±) انحراف استاندارد از میانگین به ما می دهد.

ارائه انحراف استاندارد برای بسیاری از زمینه های آماری الزامی ست. در واقع این پارامتر یکی از شاخصه های اصلی آمار توصیفی ست. اما در بسیاری از مواقع هدف اصلی پژوهشگر صرفاً توصیف داده‌های نمونه  یا به دست آوردن شاخصه های آمار توصیفی نیست بلکه هدف اصلی تعمیم نتایج نمونه به جامعه هدف یا آمار استنباطی است. به همین دلیل لازم است نتایج نمونه از اعتبار (Reliability) کافی برخوردار باشند به عبارت دیگر اگر نمونه دیگری به جز آن نمونه به تصادف از همان جامعه انتخاب و نتایج (مثلاً آماره‌هایی مانند میانگین یا درصد احتمال و سایر آماره‌ای مورد ادعا) محاسبه شود نتایج به دست آمده باید با نتایج نمونه قبل تفاوت چندانی نداشته باشد. بررسی این موضوع از طریق محاسبه شاخص خطای استاندارد صورت می‌گیرد.

مقالات زیر در درک بهتر اصطلاحات تخصصی و فهم عمیق تر انحراف استاندارد و خطای استانداردکمک می کنند.

انحراف استاندارد

آمار در آنالیزهای شیمیایی

آزمون های معناداری