روش های دسته بندی بر خلاف روش های خوشه بندی براساس مدل سازی عمل می کنند. انواع روش های دسته بندی برای جحل مسایل و مشکلات مختلف برای آنالیز داده ها به کار می روند. این روش ها بسیار متنوع هستند. ما از انواع روش های دسته بندی مختلف چند روش متداول را در اینجا به اختصار شرح داده ایم.

تجزیه مولفه های اصلی (PCA)

یکی از متداول ترین روش های تشخیص الگو و خوشه بندی روش تجزیه مولفه های اصلی (principal component analysis) با نام اختصاری و متداول PCA است. این روش در بسیاری از زمینه های علوم شامل بیولوژی، کشاورزی، اقتصاد، گرافیک، شیمی، علوم اجتماعی و رفتاری و غیره جهت تشخیص الگو (pattern recognition)، دسته بندی (Clustering) و طبقه بندی (classification)، مدل سازی نرم (soft modeling) و ..کاربرد گسترده ای دارد. این روش اگرچه جزو روش های یادگیری با نظارت نیست و برای دسته بندی به کار نمی رود اما به دلیل این که مبنای و اساس بسیاری از روش های دسته بندی ست قبل از معرفی روش های دسته بندی توضیحی در مورد این روش ارائه می شود. برای آشنایی با این روش این مقاله را بخوانید.

تکنیک‌های تمایزی

تکنیک‌های طبقه‌بندی تمایزی (Discriminant Classification Techniques) از اولین انواع روش های دسته بندی هستند که منجر به مدل‌هایی می‌شوند که هر نمونه ناشناخته را بر اساس بردار اندازه‌گیری‌های مورد استفاده برای توصیف آن به یکی از G کلاس‌های داده شده اختصاص می‌دهند. با استفاده از یک فرمول ریاضی دقیق‌تر، xi یک بردار v بعدی که از داده‌های تجربی اندازه‌گیری شده در نمونه iام تشکیل شده تعریف می شود. سپس روش تمایزی موردنظر با یافتن رابطه بین بردار و یک متغیر کیفی یا y که براساس دسته‌های موجود کدگذاری می شود، عمل می‌کند.

آنالیز تمایزی خطی (LDA) و درجه دوم (QDA)

از نظر تاریخی، اولین روش طبقه بندی که در مقاله ها ارائه شد، آنالیز تمایزی خطی (linear discriminant analysis) با نام متداول LDA بود که توسط فیشر در سال 1936 معرفی شد. LDA یک روش احتمالی است. و فرض بر این است که احتمال تعلق یک نمونه به یک کلاس خاص از توزیع گاوسین چند متغیره تبعیت می‌کند و به عنوان فرمول قانون طبقه‌بندی، نیاز به محاسبه این احتمال دارد. از نقطه نظر هندسی، این مربوط به تعریف سطوح تصمیم گیری  است که ابرفضای v بعدی را به مناطق G مربوط به کلاس های مختلف تقسیم می کند. ابرسطح هایی (hypersurface) که مناطق فضای چند بعدی مربوط به کلاس های مختلف را از هم جدا می کنند، خطی هستند . علت نام گذاری LDA خطی بودن این ابرسطح های جدا کننده کلاس ها از هم هستند.

LDA یا آنالیزتمایزی نرمال (Normal Discriminant Analysis) یک تکنیک کاهش ابعاد نیز است که معمولاً برای مسائل طبقه بندی نظارت شده استفاده می شود. برای نمایش ویژگی ها در فضای ابعاد بالاتر به فضای با ابعاد پایین تر استفاده می شود. LDA از هر دو محور (x,y) برای ایجاد یک محور جدید استفاده می‌کند و داده‌ها را بر روی یک محور جدید به روشی برای به حداکثر رساندن تفکیک دو دسته و در نتیجه، کاهش گراف دو بعدی به یک نمودار یک بعدی، تصویرسازی (project) می کند. دو معیار توسط LDA برای ایجاد یک محور جدید استفاده می شود:

• به حداکثر رساندن فاصله بین میانگین های دو کلاس
• حداقل کردن فاصله درون یک کلاس

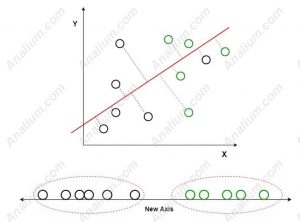
شکل 1- نحوه کاهش داده در روش LDA

در شکل بالا مشاهده می شود که یک محور جدید (به رنگ قرمز) در نمودار دو بعدی ایجاد و رسم شده است به طوری که فاصله بین میانگین های دو کلاس را به حداکثر می رساند و تغییرات در هر کلاس را به حداقل می رساند. به زبان ساده، این محور جدید ایجاد شده، جدایی بین نقاط داده دو کلاس را افزایش می دهد. پس از ایجاد این محور جدید با استفاده از معیارهای ذکر شده، تمامی نقاط داده کلاس ها بر روی این محور جدید رسم شده و در شکل پایین نشان داده شده است.

اساس روش آنالیز تمایزی درجه دوم (Quadratic Discriminant Analysis) یا QDA مشابه روش LDA است با این تفاوت که QDA طبقه بندی کننده قوی تری ارائه می کند که می تواند مرزهای غیر خطی (شامل هایپر بیضی، هایپرکره، هایپرپارابولوئید) را در فضای ویژگی ثبت کند. بنابراین، محدودیت کمتری نیز دارد، ولی نیاز به آنالیز دقیق تری دارد تا اطمینان حاصل شود که مدل بیش از حد برازش(overfit)  نشده است.

آنالیز تمایزی حداقل مربعات جزئی (PLS-DA)

وقتی مجموعه داده‌ها بر روی مجموعه‌ای از متغیرهای پنهان (latent variables) پیش‌بینی می‌شود، مانند مورد تجزیه و تحلیل مؤلفه‌های اصلی یا PCA نمونه‌ها را در یک فضای فرعی با ابعاد کاهش‌یافته بدست می‌آوریم که به صورت محورهای متعامد یا عمود برهم که همبستگی با هم ندارند تبدیل می شوند. (این دقیقاً همان چیزی است که در مورد روش آنالیز تمایزی حداقل مربعات جزئی (Partial least squares-discriminant analysis) یا PLS-DA اتفاق می افتد

این روش مشابه روش حداقل مربعات جزئی یا PLS در روش های رگرسیونی ست. با کدگذاری مناسب اطلاعات مربوط به کلاس به یک ماتریس وابسته Y، هر روش رگرسیونی را می توان به یک روش طبقه بندی تبدیل کرد. در آنالیز تمایزی حداقل مربعات جزئی (Partial least squares-discriminant analysis) یا PLS-DA ماتریس پاسخ Y کیفی است و به صورت یک ماتریس که عضویت هر مشاهده یا نمونه را کد گذاری می کند تعریف می شود. سپس روش PLS  بر روی ماتریس X و  Y به نحوی اجرا می‌شود که گویی Y یک ماتریس پیوسته است و در عمل برای مجموعه‌های داده بزرگ که در آن LDA و QDA با مشکل همبستگی متغیرها مواجه هستند، عملکرد بسیار خوبی دارد. الگوریتم PLS-DA یک طبقه‌بندی‌کننده خطی است.

k– نزدیک ترین همسایه (KNN)

الگوریتم k- نزدیک ترین همسایه (k-Nearest neighbors) با نام متداول KNN یک روش مفهومی و الگوریتمی بسیار ساده است که امکان عملیات طبقه بندی غیرخطی را فراهم می کند و علیرغم سادگی آن، در بسیاری از موارد این روش می تواند نتایج قابل اعتمادی را حتی زمانی که روش های پیچیده تر شکست می خورند ارائه دهد. این روش یک روش ناپارامتریک مبتنی بر فاصله است که هر شی ناشناخته را به دسته ای که اکثر k نزدیکترین نمونه های آموزشی آن (نزدیک ترین همسایگان) به آن تعلق دارند، اختصاص می دهد. مفهوم همسایگی از نظر ریاضی با برخی معیارهای شباهت بیان می شود که رایج ترین آن فاصله اقلیدسی در فضای چند متغیره است.

مدل‌سازی مستقل نرم قیاس‌های طبقاتی (SIMCA)

SIMCA مدل‌سازی مستقل نرم قیاس‌های طبقاتی (SIMCA)  با نام متداول سیمکا که در ابتدا توسط Wold در سال 1976 پیشنهاد شد. در این روش هر کلاس از نمونه‌ها به طور جداگانه با مدل مؤلفه اصلی (PCA) خود توصیف می‌شود. بنابراین، در اصل، هر درجه ای از همخطی داده ها را می توان توسط مدل ها تطبیق داد. همان طور که در بخش PCA نوشته شد، هنگامی که اشیاء (objects) داده به یک فضای جزء اصلی (PC) تصویرسازی می‌شوند، فواصل محاسبه و به عنوان بخشی از نتایج PCA ارائه می‌شوند. فاصله اقلیدسی در فضای متغیر بیشترین استفاده را برای اندازه گیری شباهت بین نمونه ها یا اشیاء را دارد.

شکل زیر روش SIMCA را برای یک دسته بندی دوتایی نشان میدهد. نمونه ها یا اشیاء گروه اول با دو PC مدل سازی می شوند  و نمونه ها یا اشیاء گروه دوم با یک PC مدل سازی می شود (a). یک نمونه یا شی جدید، O، (نقطه قرمز در شکل b) در فضا هر دو مدل مقایسه می شود. این مقایسه براساس فاصله نمونه جدید با PC های هر دو گروه انجام می شود. بر اساس میزان فاصله این نمونه جدید گروه یا کلاس  آن مشخص می شود.

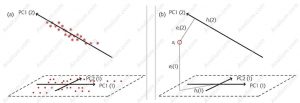
شکل 2- روش SIMCA را برای یک دسته بندی دوتایی

شبکه عصبی مصنوعی

برای آشنایی با اصول شبکه عصبی مصنوعی و انواع آن اینجا را ببینید.

ماشین بردار پشتیبان

ماشین‌های بردار پشتیبان (Support vector machines) یا SVM مجموعه‌ای از روش‌های یادگیری تحت نظارت هستند که برای طبقه‌بندی، رگرسیون و تشخیص نقاط پرت استفاده می‌شوند. ماشین های بردار پشتیبان روش موثر برای داده های و فضاهای با ابعا زیاد هستند و زمانی که ویژگی ها بیشتر از نمونه ها باشد نیز همچنان عملکرد خوبی دارند.

هدف از الگوریتم ماشین بردار پشتیبان، یافتن یک ابر صفحه (Hyperplane) در یک فضای N بعدی (N – تعداد ویژگی ها) است که به طور مشخص نقاط داده را طبقه بندی می کند. برای جدا کردن دو دسته از نقاط داده، ابرصفحه های ممکن زیادی وجود دارد که می توان انتخاب کرد. هدف ما این است که صفحه ای را پیدا کنیم که حداکثر حاشیه (margin)، یعنی حداکثر فاصله بین نقاط داده هر دو کلاس را داشته باشد. به حداکثر رساندن فاصله حاشیه مقداری تقویت را فراهم می کند تا بتوان نقاط داده آینده را با اطمینان بیشتری طبقه بندی کرد.

 

 

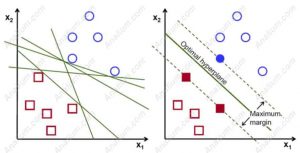
ابر صفحه ها مرزهای تصمیم گیری هستند که به طبقه بندی نقاط داده کمک می کنند. نقاط داده ای که در دو طرف ابر صفحه قرار می گیرند را می توان به کلاس های مختلف نسبت داد. همچنین، ابعاد ابر صفحه به تعداد ویژگی ها بستگی دارد. اگر تعداد ویژگی های ورودی 2 باشد، آنگاه ابر صفحه فقط یک خط است. اگر تعداد ویژگی های ورودی 3 باشد، ابر صفحه به یک صفحه دو بعدی تبدیل می شود. تصور زمانی که تعداد ویژگی ها از 3 بیشتر شود دشوار می شود.

بردارهای پشتیبان نقاط داده ای هستند که به ابر صفحه نزدیکتر هستند و بر موقعیت و جهت ابر صفحه تأثیر می گذارند. با استفاده از این بردارهای پشتیبانی، حاشیه طبقه بندی کننده را به حداکثر می رسانیم. حذف بردارهای پشتیبانی موقعیت ابر صفحه را تغییر می دهد. اینها نکاتی هستند که به ما در ساخت SVM کمک می کنند.

SVM می تواند دو نوع باشد: خطی و غیر خطی. نوع خطی برای داده‌های قابل جداسازی خطی استفاده می‌شود، به این معنی که اگر یک مجموعه داده را بتوان با استفاده از یک خط مستقیم به دو کلاس طبقه‌بندی کرد، آن‌گاه این داده‌ها به عنوان داده‌های جداپذیر خطی نامیده می‌شوند و طبقه‌بندی کننده به عنوان طبقه‌بندی کننده SVM خطی استفاده می‌شود. روش غیر خطی برای داده های جدا شده به صورت غیر خطی استفاده می شود، به این معنی که اگر یک مجموعه داده را نتوان با استفاده از یک خط مستقیم طبقه بندی کرد، این داده ها را داده های غیر خطی و طبقه بندی کننده استفاده شده را غیر خطی می نامند.

برای آشنایی بیشتر با مباحث مرتبط با روش های دسته بندی مقالات زیر را ببینید:

اصول روش ها ی دسته بندی

انواع روش ها ی دسته بندی

ارزیابی و اعتبار سنجی روش های دسته بندی