رگرسیون خطی چندگانه (MLR) چیست؟

رگرسیون خطی چندگانه (Multiple linear regression) با نام متداول MLR که به سادگی به عنوان رگرسیون چندگانه نیز شناخته می شود، یک تکنیک آماری است که از چندین متغیر توضیحی برای پیش بینی نتیجه یک متغیر پاسخ استفاده می کند. هدف رگرسیون خطی چندگانه مدل سازی رابطه خطی بین متغیرهای توضیحی (مستقل) و متغیرهای پاسخ (وابسته) است. در اصل، رگرسیون چندگانه گسترش رگرسیون حداقل مربعات معمولی (ordinary least-squares ) یا OLS است زیرا شامل بیش از یک متغیر توضیحی است.

آنچه که رگرسیون خطی چندگانه می تواند به ما بگوید

رگرسیون خطی ساده (Simple linear regression) تابعی است که به یک تحلیلگر یا آماردان اجازه می دهد تا بر اساس اطلاعاتی که در مورد یک متغیر دارد، متغیردیگر را پیش بینی کند. رگرسیون خطی تنها زمانی قابل استفاده است که دو متغیر پیوسته باشند – یک متغیر مستقل و یک متغیر وابسته. متغیر مستقل پارامتری است که برای محاسبه متغیر وابسته یا نتیجه استفاده می شود. یک مدل رگرسیون چندگانه به چندین متغیر توضیحی گسترش می یابد.

رگرسیون خطی چندگانه (MLR) برای تعیین یک رابطه ریاضی بین چندین متغیر تصادفی استفاده می شود. به عبارت دیگر، MLR بررسی می کند که چگونه چندین متغیر مستقل با یک متغیر وابسته مرتبط هستند. هنگامی که هر یک از عوامل مستقل برای پیش‌بینی متغیر وابسته تعیین شد، می‌توان از اطلاعات مربوط به متغیرهای متعدد برای ایجاد پیش‌بینی دقیق در سطح تأثیری که بر متغیر نتیجه می‌گذارند استفاده کرد. مدل رابطه ای را به شکل یک خط مستقیم (خطی) ایجاد می کند که به بهترین وجه تمام نقاط داده فردی را تخمین می زند.

برای تخمین رابطه بین دو یا چند متغیر مستقل و یک متغیر وابسته از رگرسیون خطی چندگانه استفاده می شود. به عنوان مثال اگر بخواهیم بدانیم که: رابطه بین دو یا چند متغیر مستقل و یک متغیر وابسته چقدر قوی است (مثلاً چگونگی تأثیر بارندگی، دما و مقدار کود افزوده شده بر رشد محصول) و یا مقدار متغیر وابسته در مقدار معینی از متغیرهای مستقل (مثلاً عملکرد مورد انتظار یک محصول در سطوح معینی از بارندگی، دما و افزودن کود).

مفروضات مدل رگرسیون خطی چندگانه

• همگنی واریانس یا همسانی (Homogeneity of variance or homoscedasticity): این فرض بر این اساس است که اندازه خطا در پیش بینی ما به طور قابل توجهی در مقادیر متغیر مستقل تغییر نمی کند.

2. استقلال مشاهدات (Independence of observations) – این فرض بیان می کند که مشاهدات درون داده های ما مستقل از یکدیگر هستند و از طریق روش های آماری معتبر جمع آوری شده اند.

چند خطی بودن (multicollinearity): در رگرسیون خطی چندگانه، ممکن است برخی از متغیرهای توضیحی شما با یکدیگر همبستگی داشته باشند. این به چند خطی معروف است. به عنوان مثال، قد و وزن به شدت با هم مرتبط هستند. اگر هر دو این متغیرها برای پیش‌بینی جنسیت استفاده می‌شوند، ما باید فقط از یکی از این متغیرهای مستقل در مدل خود استفاده کنیم، زیرا این می‌تواند اطلاعات اضافی ایجاد کند و نتایج را در مدل رگرسیونی ما منحرف کند.

3. نرمال بودن (Normality): فرض می کنیم که داده های ما به طور معمول توزیع شده اند.
4. خطی بودن (Linearity): رگرسیون خطی چندگانه مستلزم خطی بودن رابطه بین متغیرهای مستقل و وابسته است.

فرمول و محاسبه MLR

روش MLR از رابطه کلی زیر برای ایجاد یک رابطه بین چند متغیر مستقل و متغیر وابسته استفاده می کند:

i=n تعداد مشاهدات

yi = متغیر وابسته

xi = متغیرهای توضیحی

β0 = y-فاصله (ترم ثابت)

βp = ضرایب شیب برای هر متغیر توضیحی

ϵ = عبارت خطای مدل (همچنین به عنوان باقیمانده شناخته می شود)

برآوردهای حداقل مربعات (,B2…Bp  B1، B0) معمولاً توسط نرم افزارهای آماری محاسبه می شوند. به همان اندازه متغیرها را می توان در مدل رگرسیونی گنجاند که در آن هر متغیر مستقل با اعداد 1،2، 3، 4…p متمایز می شود. مدل رگرسیون چندگانه به تحلیلگر اجازه می دهد تا بر اساس اطلاعات ارائه شده بر روی متغیرهای توضیحی چندگانه، یک نتیجه را پیش بینی کند.

برای یافتن بهترین خط برای هر متغیر مستقل، رگرسیون خطی چندگانه سه چیز را محاسبه می‌کند:

• ضرایب رگرسیون که منجر به کوچکترین خطای کلی مدل می شود.
• آماره t مدل کلی (t-statistic)
• .مقدار p مرتبط (اگر فرضیه صفر مبنی بر عدم وجود رابطه بین متغیرهای مستقل و وابسته درست باشد، چقدر احتمال دارد که آمار t به طور تصادفی رخ دهد).

با این حال، مدل همیشه کاملاً دقیق نیست زیرا هر نقطه داده می تواند کمی با نتیجه پیش بینی شده توسط مدل متفاوت باشد. مقدار باقیمانده، E، که تفاوت بین نتیجه واقعی و نتیجه پیش بینی شده است، در مدل گنجانده شده است تا چنین تغییرات جزئی را در نظر بگیرد.

ضریب تعیین (coefficient of determination) یا همان R-squared یک متریک آماری است که برای اندازه‌گیری اینکه چقدر از تغییرات در نتیجه را می‌توان با تغییر در متغیرهای مستقل توضیح داد، استفاده می‌شود. R2 همیشه با اضافه شدن پیش‌بینی‌کننده‌های بیشتری به مدل MLR افزایش می‌یابد، حتی اگر پیش‌بینی‌کننده‌ها به متغیر نتیجه مرتبط نباشند.

بنابراین، R² به خودی خود نمی‌تواند برای شناسایی اینکه کدام پیش‌بینی‌کننده‌ها باید در یک مدل گنجانده شوند و کدام‌ها باید کنار گذاشته شوند، استفاده شود. R² فقط می تواند بین 0 و 1 باشد، مقدار  0 نشان می دهد که نتیجه توسط هیچ یک از متغیرهای مستقل قابل پیش بینی نیست و 1 نشان می دهد که می توان نتیجه را بدون خطا از متغیرهای مستقل پیش بینی کرد.

هنگام تفسیر نتایج رگرسیون چندگانه، ضرایب بتا (β) را باید مورد توجه قرار داد. بزرگی و علامت این ضرایب نشان دهنده تاثیر متغیر مستقل بر روی پاسخ یا نتیجه را نشان می دهد. خروجی یک رگرسیون چندگانه را می توان به صورت افقی به صورت معادله یا به صورت عمودی به شکل جدول نمایش داد.

تفاوت بین رگرسیون خطی و چندگانه

رگرسیون مربع های خطی معمولی (OLS) پاسخ یک متغیر وابسته را با توجه به تغییر در برخی از متغیرهای توضیحی مقایسه می کند. با این حال، یک متغیر وابسته به ندرت تنها با یک متغیر توضیح داده می شود. در این مورد، یک تحلیلگر از رگرسیون چندگانه استفاده می کند، که سعی می کند یک متغیر وابسته را با استفاده از بیش از یک متغیر مستقل توضیح دهد. رگرسیون های چندگانه می توانند خطی و غیرخطی باشند. شکل 1 تفاوت دو مدل رگرسیون خطی چندگانه و ساده را نشان می دهد. در این شکل MLR برای دو متعیر (X1,X2) نشان داده شده است.

 

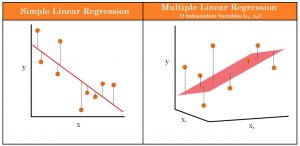
در رگرسیون خطی چندگانه، مدل خط بهترین برازش را محاسبه می‌کند که واریانس هر یک از متغیرهای موجود در ارتباط با متغیر وابسته را به حداقل می‌رساند. از آنجایی که با یک خط مطابقت دارد، یک مدل خطی است. همچنین مدل‌های رگرسیون غیرخطی شامل چندین متغیر مانند رگرسیون لجستیک (logistic regression)، رگرسیون درجه دوم (quadratic regression) وجود دارد.

یک متغیر وابسته به ندرت تنها با یک متغیر توضیح داده می شود. در چنین مواردی، یک تحلیلگر از رگرسیون چندگانه استفاده می کند، که سعی می کند یک متغیر وابسته را با استفاده از بیش از یک متغیر مستقل توضیح دهد. با این حال، مدل فرض می کند که هیچ همبستگی عمده ای بین متغیرهای مستقل وجود ندارد.