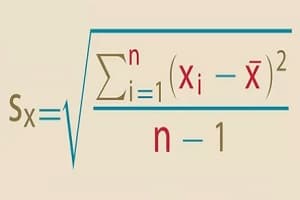آنالیز واریانس یا تحلیل واریانس (Analysis of variance)، با کلمه مخفف آنووا (ANOVA)، از مباحث بسیار کاربردی و پرتکرار آماری ست که برای مقایسه میانگین چند گروه به کار می رود. مانند آزمون های آماری که در مقاله های قبلی بحث شد، تحلیل واریانس یک‌طرفه و تحلیل واریانس دوطرفه از انواع روش های تحلیل واریانس هستند. تحلیل واریانس از آزمون‌‌های فیشر (تست F) برای بررسی برابر بودن میانگین‌ها استفاده می‌کند که متعلق به سه یا تعدادی بیشتر از گروه‌ها هستند.  آنالیز واریانس در واقع یک آزمون F دو بعدی (two dimensional F-test) ست و از نظر مفهومی بسیار شبیه به تست F است. در واقع باید آزمون F را بر روی تمام زوج های ممکن همه گروه ها انجام داد. این کار برای تعداد متغیر زیاد بسیار پیچیده و خسته کننده است. بنابراین ابتدا آزمون فیشر یا آزمون F شرح داده می شود.

تست F

آزمون F (F-Test) ، که بعضی مواقع با اسم مبدع آن رونالد فیشر به تست فیشر یا آزمون فیشر هم شناخته می شود، امکان مقایسه واریانس دو مجموعه داده مختلف برای تعیین تفاوت آماری معنی دار را فراهم می کند. در یک آزمایشگاه معمولا مجموعه داده هایی است که تحت شرایط مختلف به دست می آیند، زیاد هستند. به عنوان مثال، آزمایش هایی که در روزهای مختلف انجام شده است، مقایسه عملکرد دو روش متفاوت یا دو دستگاه آنالیزی مختلف برای آنالیزهای یکسان، مقایسه عملکرد دو آنالیست که اندازه گیری های یکسانی را انجام می دهند و غیره. هنگامی که نتایج نهایی متفاوت هستند، ما به روشی نیاز داریم که تعیین کند اختلاف از نظر آماری قابل توجه است یا خیر. به روشی مشابه آزمون Grubb و Q-test، ما با محاسبه مقدار F آزمایشی (F_exp)  و مقایسه آن با مقدار F بحرانی (F_crit)، یک F-test انجام می دهیم. اگر F_exp> F_crit واریانس دو مجموعه داده مورد استفاده برای از نظر آماری متفاوت است.

برای به دست آوردن F آزمایشی (F_exp) از رابطه زیر استفاده می شود:

F_(exp)= S²₁/S²2

F_exp با نسبت واریانس نمونه (مربع انحراف معیار) تعیین می شود. مقدار واریانس بزرگ تر در عدد قرار می گیرد تا F_exp همیشه بزرگ تر از یک باشد.

در این حالت، فرضیه صفر این است که این دو واریانس جمعیت یکسانی را نشان می دهند. برای رد (یا پذیرفتن) فرضیه صفر، F_exp را با F_crit مقایسه می کنیم. جداول مقادیر F_crit بر حسب  تابعی از سطح اطمینان (اغلب 95%) و درجه آزادی برای واریانس ها جدول بندی شده اند. خوشبختانه امروزه نیازی به مراجعه به جدول های آماری نداریم. چون نرم افزارهای آماری مقادیر آماره هایی بحرانی را در محاسبات نهایی حود نشان می دهند بنابراین اکثر مواقع نیازی به مراجعه به جدول های آماری نیست.

ANOVA

همان طور که گفته شد، آنالیز واریانس در واقع یک آزمون F دو بعدی ست و از نظر مفهومی بسیار شبیه به تست F است. در واقع باید آزمون F را بر روی تمام زوج های ممکن همه گروه ها انجام داد. این کار برای تعداد متغیر زیاد بسیار پیچیده و خسته کننده است. اما آنالیز واریانس یک روش موجه تری برای مقایسه واریانس جمعیت های چندین گروه است. در آنالیز واریانس هم در واقع ما یک مقدار F را در تجزیه و تحلیل محاسبه می کنیم. به عنوان مثال، در مثال بالا ، دقت دو روش آنالیزی با هم مقایسه شد اما اگر بخواهیم بین تعداد بیشتر روش آنالیزی مقایسه انجام دهیم ( بیشتر از دوتا) و نتایج را از نظر آماری مقایسه کنیم باید از ANOVA استفاده کنیم.

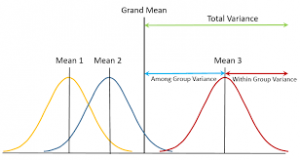
محاسبه ANOVA  و مراحل انجام آن

• محاسبه میانگین بزرگ (grand mean)
• محاسبه مجموع مربعات تمام داده ها (sum of squares of all the observations) برحسب میانگین کل
• محاسبه مجموع مربعات هر گروه از میانگین بزرگ (the sum of squares (deviations) of the group means from the grand mean,)
• محاسبه مجموع مجموع مربعات هر گروه (the sum over the sums of squared deviations of scores around their group’s mean)
• رسم جدول ANOA و به دست آوردن نسبت F
• تفسیر و تحلیل نتایج جدول ANOVA

شاید به نظر برسد که با فراوانی زیاد انواع نرم افزارهای رایگان و تجاری که فقط با چند کلیک نتایج را می توان بدون دردسر فهم این معادله های عجیب و غریب ارائه می کنند لزومی به جزییات ریاضی و روابط آنها نباشد. اما باید در نظر دشته باشیم که تفسیر نهایی این آزمون از محاسبه آنها بسیار مهم تر هستند و دانستن و آگاهی از مراحل محاسبه آماره ها و آزمون های معرفی شده در فهم و تفسیر درست نتایج بسیار موثر هستند. ضمن این که روابط و معادلات بالا بسیار ساده هستند فقط وقتی برای تعداد داده های زیاد به کار می روند ترسناک به نظر می رسند!!.

مقایسه  آزمون T و  ANOVA

آزمون T مواقعی به کار می رود که بخواهیم بدانیم آیا تفاوت قابل توجهی بین دو گروه وجود دارد یا خیر. در صورتی که ANOVA تعیین می کند که سه یا چند جمعیت از نظر آماری از یکدیگر متفاوت باشند. به زبان ساده وقتی مقایسه میانگین بین دو گروه مطح باشد از آزمون T و وقتی بیشتر از دو گروه باشد از ANOVA استفاده می شود. آزمون t مقایسه میانگین هاست، در حالی که ANOVA واریانس بین جمعیت ها را مقایسه می کند.

به جای آنالیز ANOVA  می توان سری های جفت شده تست t بر روی داده ها  انجام داد اما با افزایش تعداد گروه ها، ممکن است در نهایت با مقایسه های جفتی زیادی مواجه شویم که مسوله را بیشتر پیچیده خواهند کرد.

هر دو روش زمانی انجام می شوند که 1) نمونه ها از یکدیگر مستقل باشند و 2) توزیع نرمال (یا تقریبا نرمال) داشته باشند یا تعداد نمونه زیاد باشد (تعداد نمونه ها در هر گروه بیشتر از 30 باشد). نمونه های بیشتر بهتر هستند، اما آزمایشات را می توان با حداقل 3 نمونه در هر شرایط انجام داد.

برای اطلاعات بیشتر و مثال های کاربردی مقاله زیر را بخوانید:

آزمون های معناداری